Accelerated 2D optical simulation of LEDs allows quicker validation of architectural improvements (MAGAZINE)
This article was published in the April 2013 issue of LEDs Magazine.
View the Table of Contents and download the PDF file of the complete April 2013 issue, or view the E-zine version in your browser.
+++++
The limited extraction efficiency of LEDs is due to the fact that the light is generated inside media with a high refractive index and that total internal reflection occurs at the air interface. As a result, only a small portion of the light within the cone formed by the critical angle can be extracted into air, and the majority is trapped inside. The theoretical limit of the extraction efficiency is 1⁄4n2 (where n is the refractive index of the medium), which is only about 2% for GaAs-LEDs and 4% for GaN-LEDs.
To break through the theoretical limit, researchers are trying to manipulate the LED structure to extract more light. To accomplish this, many researchers rely on a trial-and-error approach to the design process. For example, S. David Roh from LG Innotek reported iterating as many as several hundred times in a paper at the Asia Communication and Photonics Conference last year. Although most designers may acknowledge that simulation software can reduce the design cycle and save time and money, not all designers use simulation tools in their practical design, perhaps because of the complexity of LED simulation problems or because they have not yet found an efficient, user-friendly simulation tool.
Still, a full 3D FDTD simulation is very expensive in terms of computation time and computer memory. One simulation for a typical LED structure could use tens of gigabytes of RAM and take a few hours on a multi-core computer. For multiple scans over wavelength, position, and polarization, it is very common for a simulation to take a few days.
To increase efficiency and make the simulation more affordable, we recently proposed and briefly reported a simplified approach in a paper at the Asia Communication and Photonics Conference. Instead of simulating a full 3D structure, we assume that the LED device is circularly symmetric so that we can perform a 2D radial simulation. The simulation effort, including both computation time and computer memory, can be reduced by hundreds or even thousands of times.
General simulation procedure
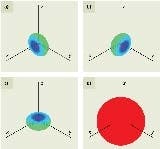
Unpolarized light is uniformly polarized in all directions. To create such a source, we can separately simulate the three orthogonal polarizations and sum the results. Shown in Fig. 1 are the far fields (also called radiation patterns) of a dipole polarized in three different directions, as well as the sum of all polarizations.
It is clearly shown that the radiation pattern of each dipole is polarization-dependent, and their sum is uniform in all directions and polarization-independent. Therefore, for each point source, three separate simulations for different orthogonal polarizations are needed. For certain types of LEDs, photons may not radiate evenly in all directions. For instance, in a GaN-based LED, there is no radiation in the crystal axis, so simulating two lateral polarizations is sufficient.
Temporal coherence
The temporal coherence of light, which is measured by a coherent length, is inversely proportional to the spectral width. Due to the dominance of spontaneous emission, as shown in Fig. 2, an LED has a much wider emission spectrum than a laser. The extraction efficiency and radiation pattern of an LED are wavelength dependent, as shown for a simulated example in Fig. 2.
The final extraction efficiency R and far-field pattern ψ(θ,φ) can be obtained by averaging the wavelength-dependent results R(λi) and ψ(θ,φ,λi) at each sampled wavelength λi, weighted by the LED radiation spectrum S(λi), that is,
where N is the number of the sampled points. The combined results are shown in Fig. 3.
2D approximation
For a typical 3D structure, a full simulation based on the preceding procedure could take a few days with tens of gigabytes of memory in order to obtain reasonable results. Such a simulation certainly limits the ability of design automation. Is there a more efficient way to simulate LEDs, even if it is an approximated method? The answer might be 2D approximation, which is appropriate for most photonic device simulations. For LEDs, however, 2D approximation oversimplifies the problem.
Radial approximation
We can improve the 2D results using a radial approximation. The commonly used 2D PhC patterns, either hexagonal or square lattices, are approximations to circular Bragg gratings, which create bandgaps in the lateral directions to force the trapped light to travel in a vertical direction. Therefore, 2D radial approximation is closer to the real problem geographically, as shown in Fig. 6.
To validate the 2D radial simulation, we first tested a flat structure, for which the 2D radial approximation is exactly the same as the original 3D structure, which is confirmed by the simulation results shown in Fig. 7. The 2D radial simulation produces almost the same results as the 3D simulation, and the discrepancy is purely numerical because of grid shapes. For the sake of comparison, the 2D results, with the line sources, are shown in the same chart, and they are very different from the 3D results.
Still, a 2D radial simulation is a good approximation to real 3D LED problems, and it produces results that are similar to those of a 3D simulation. The computation effort, for both time and memory, is usually several orders of magnitude smaller. A 3D simulation for a typical LED structure could take a few days and use tens of gigabytes of memory, and a 2D radial simulation takes only minutes and uses very little memory.
Although it is an approximation, the 2D method can still provide design insight and prove the design concept quickly. We do not expect that 3D simulation could be completely replaced by 2D radial simulation, as 3D simulation still serves as a verification tool for the final design. Also, the LED Utility can be used to perform 3D simulation as the LED designer closes on an architectural development project.